- karunia untuk menjadi rasul (1 Korintus 12:28, dan Efesus 4:11)
- karunia untuk bernubuat (Roma 12:6, 1 Korintus 12:10, 28, Efesus 4:11)
- karunia untuk mengajar (Roma 12:7, 1 Korintus 12:28, Efesus 4:11 karunia mengajar dan pastoral)
- karunia untuk memberitakan Injil (Efesus 4:11, bandingkan dengan 2 Timotius 4:5)
- karunia untuk melayani (Roma 12:7)
- karunia untuk membagi-bagikan sesuatu dan menunjukkan kemurahan (Roma 12:8)
- karunia untuk memimpin (Roma 12:8 bandingkan dengan 1 Korintus 12:28)
- karunia untuk mengusir setan (Roma 12:8)
- karunia untuk berkata-kata dengan penuh kebijaksanaan (1 Korintus 12:8)
- karunia untuk berkuasa (1 Korintus 12:10)
- karunia untuk menyembuhkan (1 korintus 12:9)
- karunia untuk berbahasa roh (1 Korintus 12:10,28)
- karunia untuk menafsirkan bahasa roh (1 Korintus 12:10,28)
- karunia untuk membedakan bermacam-macam roh (1 Korintus 12:10)
Michael Christian's Blog
Jumat, 02 Mei 2014
Karunia-Karunia Roh Kudus
Sabtu, 28 September 2013
Not Balok & Angka
Struktur Not Balok
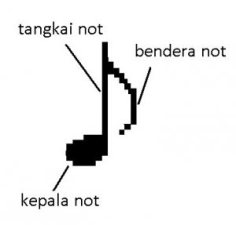
Untuk menulis not balok kita memerlukan garis-garis paranada yang berjumlah lima garis.

Di dalam paranada terdapat garis-garis yang memisahkan not-not dengan jumlah ketukan sesuai tanda birama yang ada misalnya 4/4 maka setiap 4 ketukan dipisahkan oleh garis yang disebut garis birama atau garis bar.
Pada setiap garis dan di antara garis-garis, kita tempatkan not atau nada-nada c, d, e, f, g, a, b, c dst. Penempatan sesuai dengan kunci yang kita gunakan, misalnya do=c maka pada garis 1 terletak nada 3 (mi) atau e.
Pada awal paranada biasanya kita menempatkan “kunci” yang disebut “clef”. Ada bermacam-macama clef: treble, bass, tenor, dan alto. Namun biasanya yang umum digunakan adalah clef treble dan bass.
Penggunaan clef treble dan bass secara bersamaan disebut “grand staff”
Menempatkan Not dalam Paranada.
Penempatan not-not dalam paranada harus memperhatikan kunci yang digunakan, misalnya dengan cleff treble, do=c maka kita harus menambahkan satu garis di bawah. Di bawah garis tambahan masih bisa ditambah lagi, demikian juga ke atas masih bisa ditambah lagi sesuai dengan kebutuhan not rendah atau tinggi yang dibutuhkan dalam sebuah lagu, memerlukan berapa oktaf. Satu oktaf terdiri dari 8 nada.
c, d, e, f, g, a, b, c, d, e, f, g, a, b, c, dst.

Lambang-Lambang Not Balok.
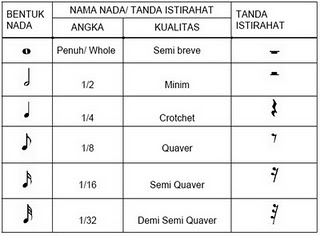
Not Penuh (1) = nada 4 ketuk. Gambar bulatan kosong.

Not Setengah (1/2) = 2 ketuk.Gambar bulatan kosong dengan tiang.

Not Seperempat (1/4) = 1 ketu. Gambar bulatan dihitamkan dengan tiang.

Not Seperdelapan (1/8) = 1/2 ketuk. Gambar bulatan dihitamkan, tiang, bendera 1.

Not Seperenambelas (1/16) = 1/4 ketuk. Gambar bulatan dihitamkan, tiang, bendera 2.

Tanda Titik.
Tanda titik ditempatkan di belakang not balok. Nilai tanda titik adalah setengah dari not di depannya. Bila not di depannya adalah not penuh (1) = 4 ketuk, maka tanda titik bernilai setengah (1/2) = 2 ketuk, dan seterusnya.

4+2=6 ketuk 2+1=3 ketuk 11/2 ketuk 3/4 ketuk
Tanda Diam
Tanda diam adalah tanda yang melambangkan sebuah lagu harus berhenti baik di tengah maupun di akhir sebuah lagu. Tanda diam dalam notasi do, re, mi, dilambangkan dengan angka 0. Dalam not balok tanda diam mempunyai lambang-lambang sesuai dengan nilai atau lamanya diam.
Tanda diam : 4 ketuk , 2 ketuk , 1 ketuk ,1/2 ,1/4
Tempo dan Dinamik.
Cressendo < artinya lagu dinyanyikan menguat / mengeras.
De Cressendo > artinya lagu dinyanyikan melembut.
Vivace artinya gembira, hidup.
Adagio artinya amat sangat lambat.
Prestissimo artinya amat sangat cepat.
Largheno artinya lambat.
Di Marcia artinya seperti orang berbaris.
Maestoso artinya khidmad, agung, dan mulia.
Con brio artinya semangat bergelora.
Allegreto artinya ringan, hidup, dan gembira.
Con bravura artinya gagah.
ff = fortissimo artinya sangat keras.
pp = pianissimo artinya sangat lambat
p = piano artinya lambat/lembut
Interval Terts & Sekunde

Penggunaan notasi balok dijelaskan dalam contoh yang diambil dari bagian awal karya Johann Strauss, An der schönen blauen Donau yang disederhanakan

Dalam notasi angka, not ditentukan dengan angka 1 (do), 2 (re), 3 (mi), 4 (fa), 5 (sol), 6 (la) dan 7 (si). Nada 1 tanpa titik merupakan nada C natural di notasi balok. Tanda satu titik di atas not, menunjukkan bahwa not tersebut naik satu birama dari nada asli, sedangkan tanda satu titik di bawah not menunjukkan bahwa not tersebut turun satu birama dari nada asli.

Notasi angka 4 suara S, A, T, B

Untuk menulis not balok kita memerlukan garis-garis paranada yang berjumlah lima garis.
Di dalam paranada terdapat garis-garis yang memisahkan not-not dengan jumlah ketukan sesuai tanda birama yang ada misalnya 4/4 maka setiap 4 ketukan dipisahkan oleh garis yang disebut garis birama atau garis bar.
Pada setiap garis dan di antara garis-garis, kita tempatkan not atau nada-nada c, d, e, f, g, a, b, c dst. Penempatan sesuai dengan kunci yang kita gunakan, misalnya do=c maka pada garis 1 terletak nada 3 (mi) atau e.
Pada awal paranada biasanya kita menempatkan “kunci” yang disebut “clef”. Ada bermacam-macama clef: treble, bass, tenor, dan alto. Namun biasanya yang umum digunakan adalah clef treble dan bass.
Penggunaan clef treble dan bass secara bersamaan disebut “grand staff”
Menempatkan Not dalam Paranada.
Penempatan not-not dalam paranada harus memperhatikan kunci yang digunakan, misalnya dengan cleff treble, do=c maka kita harus menambahkan satu garis di bawah. Di bawah garis tambahan masih bisa ditambah lagi, demikian juga ke atas masih bisa ditambah lagi sesuai dengan kebutuhan not rendah atau tinggi yang dibutuhkan dalam sebuah lagu, memerlukan berapa oktaf. Satu oktaf terdiri dari 8 nada.
c, d, e, f, g, a, b, c, d, e, f, g, a, b, c, dst.

Lambang-Lambang Not Balok.

Not Penuh (1) = nada 4 ketuk. Gambar bulatan kosong.

Not Setengah (1/2) = 2 ketuk.Gambar bulatan kosong dengan tiang.

Not Seperempat (1/4) = 1 ketu. Gambar bulatan dihitamkan dengan tiang.

Not Seperdelapan (1/8) = 1/2 ketuk. Gambar bulatan dihitamkan, tiang, bendera 1.

Not Seperenambelas (1/16) = 1/4 ketuk. Gambar bulatan dihitamkan, tiang, bendera 2.

Tanda Titik.
Tanda titik ditempatkan di belakang not balok. Nilai tanda titik adalah setengah dari not di depannya. Bila not di depannya adalah not penuh (1) = 4 ketuk, maka tanda titik bernilai setengah (1/2) = 2 ketuk, dan seterusnya.

4+2=6 ketuk 2+1=3 ketuk 11/2 ketuk 3/4 ketuk
Tanda Diam
Tanda diam adalah tanda yang melambangkan sebuah lagu harus berhenti baik di tengah maupun di akhir sebuah lagu. Tanda diam dalam notasi do, re, mi, dilambangkan dengan angka 0. Dalam not balok tanda diam mempunyai lambang-lambang sesuai dengan nilai atau lamanya diam.
Tanda diam : 4 ketuk , 2 ketuk , 1 ketuk ,1/2 ,1/4
Tempo dan Dinamik.
Cressendo < artinya lagu dinyanyikan menguat / mengeras.
De Cressendo > artinya lagu dinyanyikan melembut.
Vivace artinya gembira, hidup.
Adagio artinya amat sangat lambat.
Prestissimo artinya amat sangat cepat.
Largheno artinya lambat.
Di Marcia artinya seperti orang berbaris.
Maestoso artinya khidmad, agung, dan mulia.
Con brio artinya semangat bergelora.
Allegreto artinya ringan, hidup, dan gembira.
Con bravura artinya gagah.
ff = fortissimo artinya sangat keras.
pp = pianissimo artinya sangat lambat
p = piano artinya lambat/lembut
Interval Terts & Sekunde

Penggunaan notasi balok dijelaskan dalam contoh yang diambil dari bagian awal karya Johann Strauss, An der schönen blauen Donau yang disederhanakan

- Di sebelah kiri atas pada awal lagu biasanya ditempatkan petunjuk tempo (yaitu kecepatan lagu), seringkali dalam bahasa Italia, yang di sini menunjukkan "tempo waltz". Selain itu juga terdapat penanda metronom dalam satuan BPM (beats per minute), di sini 142 ketukan per menit.
- Tanda birama menunjukkan ritme lagu. Angka di bagian atas tanda birama menunjukkan jumlah ketukan per birama, sedangkan angka di bawah menunjukkan nilai not per ketukan. Tanda birama 3/4 di sini menunjukkan bahwa terdapat tiga ketukan dalam birama, satu ketukan kuat diikuti dua ketukan lemah, dan masing-masing ketukan bernilai not seperempat.
- Garis birama merupakan pemisah antarbirama.
- Pada bagian awal paranada terdapat kunci-G yang menandakan bahwa garis kedua dari bawah melambangkan nada g¹ (berfrekuensi sekitar 418 Hz).
- Tanda mula utama yang di sini terdiri dari dua tanda mula kres pada garis nada c dan f menunjukkan bahwa kedua nada tersebut dinaikkan setengah nada dalam semua oktaf (dimainkan sebagai nada cis dan fis) serta menunjukkan bahwa karya musik bersangkutan bertangga nada D mayor atau B minor.
- Not pertama adalah not seperempat dengan nada d1, dengan dinamika (nyaring lembutnya suara) mf (bahasa Italia, mezzo forte: agak nyaring). Dapat dilihat bahwa not tersebut langsung diikuti garis birama walaupun tiga ketuk dalam birama tersebut belum selesai. Dengan demikian, karya ini dimulai bukan dengan ketukan pertama bertekanan, melainkan dengan ketukan ketiga lemah dalam suatu birama pembuka (anacrusis).
- Not kedua juga merupakan not seperempat dan bernada d1 yang jatuh pada ketukan pertama dalam birama berikutnya.
- Tanda legato menghubungkan not d1 tersebut dengan not fis1 dan a1, menandakan bahwa ketiga not tersebut harus dimainkan secara legato (sambung-menyambung).
- Pada birama berikutnya terdapat not setengah bernada a1 berdurasi dua ketukan.
- Berikutnya terdapat not seperempat dengan dua kepala not pada posisi nada fis2 dan a2, menandakan bahwa kedua nada tersebut harus dimainkan bersamaan. Di atas not tersebut terdapat tanda staccato, menandakan bahwa not tersebut harus dimainkan secara staccato (terpisah nyata dari not sebelum dan sesudahnya).
- Tanda diam seperempat menandakan bahwa tidak ada nada yang dimainkan selama (dalam hal ini) satu ketukan.
- Di bawah tiga birama terakhir terdapat tanda decrescendo, menandakan bahwa pada ketiga birama tersebut terdapat perubahan dinamika, yaitu dimainkan makin melembut (dapat juga ditulis decresc. atau dim., diminuendo).
Dalam notasi angka, not ditentukan dengan angka 1 (do), 2 (re), 3 (mi), 4 (fa), 5 (sol), 6 (la) dan 7 (si). Nada 1 tanpa titik merupakan nada C natural di notasi balok. Tanda satu titik di atas not, menunjukkan bahwa not tersebut naik satu birama dari nada asli, sedangkan tanda satu titik di bawah not menunjukkan bahwa not tersebut turun satu birama dari nada asli.
Membaca Notasi Angka

- Do = G menunjukkan nada dasar lagu tersebut.
- 4/4 menunjukkan Tanda birama yang menunjukkan ritme lagu. Angka di bagian atas tanda birama menunjukkan jumlah ketukan per birama, sedangkan angka di bawah menunjukkan nilai not per ketukan. Tanda birama 4/4 di sini menunjukkan bahwa terdapat empat ketukan dalam birama, satu ketukan kuat diikuti tiga ketukan lemah, dan masing-masing ketukan bernilai not seperempat
- Tempo = 66 menunjukkan tempo lagu, artinya dalam satu menit ada 66 ketuk.
- SATB menunjukkan tipe suara yang menyanyikan baris tersebut.
- P berarti 'piano' yang berarti lembut, artinya lagi ini dengan dinamika yang lembut.
- Tanda Crescendo yang dilanjutkan dengan tanda decrescendo, menunjukkan ada perubahan dinamika, yakni mengeras, kemudian melembut lagi.
- Garis birama yang merupakan pemisah antar birama.
Sumber : http://galihsamudra.wordpress.com/tag/not-balok-dan-garis-paranada/
http://id.wikipedia.org/wiki/Notasi_musik
Jumat, 27 September 2013
Logaritma
Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen atau pemangkatan.
Rumus dasar logaritma:
bc= a ditulis sebagai blog a = c (b disebut basis)
Beberapa orang menuliskan blog a = c sebagai logba = c.
Basis yang sering dipakai atau paling banyak dipakai adalah basis 10


Rumus dasar logaritma:
bc= a ditulis sebagai blog a = c (b disebut basis)
Beberapa orang menuliskan blog a = c sebagai logba = c.
Basis yang sering dipakai atau paling banyak dipakai adalah basis 10


Sumber : http://id.wikipedia.org/wiki/Logaritma
Pythagoras
Rumus Pythagoras adalah rumus yang
digunakan untuk mencari panjang sisi pada sebuah segitiga siku-siku, tidak bisa untuk segitiga lainnya ( segitiga sembarang, dll ).
Penemu rumus ini adalah seorang ahli matematika dari Yunani yang bernama
Pythagoras.
Rumus :
c = garis miring
a , b = garis lurus ( bisa terbalik)
Sisi AB disebut juga dengan sisi c ,sebab berhadapan dengan sudut C.Sisi BC disebut juga dengan sisi a ,sebab berhadapan dengan sudut A.Sisi AC disebut juga dengan sisi b ,sebab berhadapan dengan sudut B.
Rumus untuk mencari panjang sisi segitiga siku-siku dengan menggunakan rumus Pythagoras adalah sebagai berikut :
 Kuadrat sisi AB = kuadrat sisi AC + kuadrat sisi BC. atau AB2 = AC2 + BC2
Kuadrat sisi AB = kuadrat sisi AC + kuadrat sisi BC. atau AB2 = AC2 + BC2
Rumus untuk mencari panjang sisi alas yaitu:a2 = c 2 - b 2
Rumus untuk mencari sisi samping yaitu:b2 = c 2 - a 2 Contoh : 1). Berapakah panjang sisi AB pada gambar di bawah ini ?

Diketahui: BC = 8cm, AC = 6cmDitanya : AB = ? Jawab: AB2 = AC2 + BC2 = 62 + 82 = 36 + 64 = 100AB = √100 = 10 Jadi panjang sisi AB adalah 10cm.
2). Berapakah panjang sisi b pada gambar di bawah ini ? Diketahui : a = 12cm , b = 13cm. Ditanya b = ?
Jawab :
Karena yang ditanyakan panjang sisi b, maka berlaku rumus :
b2 = c2 - a2
= 132 - 122
= 169 - 144
= 25b
= √25
= 5cm
Diketahui : a = 12cm , b = 13cm. Ditanya b = ?
Jawab :
Karena yang ditanyakan panjang sisi b, maka berlaku rumus :
b2 = c2 - a2
= 132 - 122
= 169 - 144
= 25b
= √25
= 5cm
3). Berapakah panjang sisi a pada gambar di bawah ini ?

Diketahui: c = 17cm , b = 8cm .Ditanya a = ? Jawab: Karena yang ditanyakan adalah panjang sisi a , maka berlaku rumus: a2 = c2 - b2 = 172 - 82 = 289 - 64 = 225 a = √225 = 15 cm
4). Sebuah persegi panjang dengan panjang 24cm dan lebar 7cm. Berapakah panjang diagonal atau AC dari bangun tersebut ?
 Jawab:
AC2 = AB2 + BC2
Jawab:
AC2 = AB2 + BC2
= 72 + 242
= 49 + 576AC
= √625 = 25cm
Sulit / malas menghitung ? hafalkan saja
( a , b , c )
* a dan b boleh terbalik / tertukar
Berlaku untuk kelipatan :
Contoh :
a = 15 ,b = 20 , c = ?
ingat ( 3, 4, 5)
sehingga a dan b bisa dibagi 5 jadi 3 dan 4
a = 3, b = 4, c = 5
setelah tau c = 5 jangan lupa a , b, c dikalikan lagi 5
sehingga (a , b ,c ) = ( 15, 20 , 25 )
Rumus :
c = garis miring
a , b = garis lurus ( bisa terbalik)
Sisi AB disebut juga dengan sisi c ,sebab berhadapan dengan sudut C.Sisi BC disebut juga dengan sisi a ,sebab berhadapan dengan sudut A.Sisi AC disebut juga dengan sisi b ,sebab berhadapan dengan sudut B.
Rumus untuk mencari panjang sisi segitiga siku-siku dengan menggunakan rumus Pythagoras adalah sebagai berikut :
 Kuadrat sisi AB = kuadrat sisi AC + kuadrat sisi BC. atau AB2 = AC2 + BC2
Kuadrat sisi AB = kuadrat sisi AC + kuadrat sisi BC. atau AB2 = AC2 + BC2Rumus untuk mencari panjang sisi alas yaitu:a2 = c 2 - b 2
Rumus untuk mencari sisi samping yaitu:b2 = c 2 - a 2 Contoh : 1). Berapakah panjang sisi AB pada gambar di bawah ini ?

Diketahui: BC = 8cm, AC = 6cmDitanya : AB = ? Jawab: AB2 = AC2 + BC2 = 62 + 82 = 36 + 64 = 100AB = √100 = 10 Jadi panjang sisi AB adalah 10cm.
2). Berapakah panjang sisi b pada gambar di bawah ini ?
 Diketahui : a = 12cm , b = 13cm. Ditanya b = ?
Jawab :
Karena yang ditanyakan panjang sisi b, maka berlaku rumus :
b2 = c2 - a2
= 132 - 122
= 169 - 144
= 25b
= √25
= 5cm
Diketahui : a = 12cm , b = 13cm. Ditanya b = ?
Jawab :
Karena yang ditanyakan panjang sisi b, maka berlaku rumus :
b2 = c2 - a2
= 132 - 122
= 169 - 144
= 25b
= √25
= 5cm
3). Berapakah panjang sisi a pada gambar di bawah ini ?

Diketahui: c = 17cm , b = 8cm .Ditanya a = ? Jawab: Karena yang ditanyakan adalah panjang sisi a , maka berlaku rumus: a2 = c2 - b2 = 172 - 82 = 289 - 64 = 225 a = √225 = 15 cm
4). Sebuah persegi panjang dengan panjang 24cm dan lebar 7cm. Berapakah panjang diagonal atau AC dari bangun tersebut ?
 Jawab:
AC2 = AB2 + BC2
Jawab:
AC2 = AB2 + BC2= 72 + 242
= 49 + 576AC
= √625 = 25cm
Sulit / malas menghitung ? hafalkan saja
( a , b , c )
* a dan b boleh terbalik / tertukar
| (3,4,5) | (5,12,13) | (7,24,25) | (8,15,17) | (9,40,41) |
| (11,60,61) | (12,35,37) | (13,84,85) | (15,112,113) | (16,63,65) |
| (17,144,145) | (19,180,181) | (20,21,29) | (20,99,101) | (21,220,221) |
| (23,264,265) | (24,143,145) | (25,312,313) | (27,364,365) | (28,45,53) |
| (28,195,197) | (29,420,421) | (31,480,481) | (32,255,257) | (33,56,65) |
| (33,544,545) | (35,612,613) | (36,77,85) | (36,323,325) | (37,684,685) |
| (39,80,89) | (39,760,761) | (40,399,401) | (41,840,841) | (43,924,925) |
| (44,117,125) | (44,483,485) | (48,55,73) | (48,575,577) | (51,140,149) |
| (52,165,173) | (52,675,677) | (56,783,785) | (57,176,185) | (60,91,109) |
| (60,221,229) | (60,899,901) | (65,72,97) | (68,285,293) | (69,260,269) |
| (75,308,317) | (76,357,365) | (84,187,205) | (84,437,445) | (85,132,157) |
| (87,416,425) | (88,105,137) | (92,525,533) | (93,476,485) | (95,168,193) |
| (96,247,265) | (100,621,629) | (104,153,185) | (105,208,233) | (105,608,617) |
| (108,725,733) | (111,680,689) | (115,252,277) | (116,837,845) | (119,120,169) |
| (120,209,241) | (120,391,409) | (123,836,845) | (124,957,965) | (129,920,929) |
| (132,475,493) | (133,156,205) | (135,352,377) | (136,273,305) | (140,171,221) |
| (145,408,433) | (152,345,377) | (155,468,493) | (156,667,685) | (160,231,281) |
| (161,240,289) | (165,532,557) | (168,425,457) | (168,775,793) | (175,288,337) |
| (180,299,349) | (184,513,545) | (185,672,697) | (189,340,389) | (195,748,773) |
| (200,609,641) | (203,396,445) | (204,253,325) | (205,828,853) | (207,224,305) |
| (215,912,937) | (216,713,745) | (217,456,505) | (220,459,509) | (225,272,353) |
| (228,325,397) | (231,520,569) | (232,825,857) | (240,551,601) | (248,945,977) |
| (252,275,373) | (259,660,709) | (260,651,701) | (261,380,461) | (273,736,785) |
| (276,493,565) | (279,440,521) | (280,351,449) | (280,759,809) | (287,816,865) |
| (297,304,425) | (300,589,661) | (301,900,949) | (308,435,533) | (315,572,653) |
| (319,360,481) | (333,644,725) | (336,377,505) | (336,527,625) | (341,420,541) |
| (348,805,877) | (364,627,725) | (368,465,593) | (369,800,881) | (372,925,997) |
| (385,552,673) | (387,884,965) | (396,403,565) | (400,561,689) | (407,624,745) |
| (420,851,949) | (429,460,629) | (429,700,821) | (432,665,793) | (451,780,901) |
| (455,528,697) | (464,777,905) | (468,595,757) | (473,864,985) | (481,600,769) |
| (504,703,865) | (533,756,925) | (540,629,829) | (555,572,797) | (580,741,941) |
| (615,728,953) | (616,663,905) | (696,697,985) |
Contoh :
a = 15 ,b = 20 , c = ?
ingat ( 3, 4, 5)
sehingga a dan b bisa dibagi 5 jadi 3 dan 4
a = 3, b = 4, c = 5
setelah tau c = 5 jangan lupa a , b, c dikalikan lagi 5
sehingga (a , b ,c ) = ( 15, 20 , 25 )
Persamaan Garis
Persamaan Garis
Jika :
1. Diketahui Gradien, dan titik
Jika diketahui gradien dan melalui titik
dan melalui titik  , kita bisa menggunakan rumus
, kita bisa menggunakan rumus  Contoh:
Contoh:
Persamaan garis lurus yang memiliki gradien dan melalui titik
dan melalui titik  adalah ….
Jawab:
adalah ….
Jawab:

2. Diketahui dua titik
Jika persamaan garis melalui titik dan
dan  , kita bisa menggunakan rumus
, kita bisa menggunakan rumus  Contoh:
Contoh:
Persamaan garis lurus yang melalui titik (1,4) dan (3,8) adalah …. Jawab:

3. Diketahui Garis dan Titik
Jika persamaan garis sejajar / tegak lurus dengan garis
sejajar / tegak lurus dengan garis  , dan melalui titik
, dan melalui titik  , maka
, maka
(i)
(ii) Jika sejajar maka
Jika tegak lurus maka atau
atau 
(iii) Melalui titik , berarti
, berarti 
Dalam hal ini, ketiga proses tersebut dapat diperingkas dengan rumus berikut:
Contoh:
Persamaan garis lurus yang tegak lurus garis dan melalu titik
dan melalu titik  adalah ….
Jawab:
adalah ….
Jawab:
Dari soal kita dapat . Sehingga persamaan garis yang kita cari adalah
. Sehingga persamaan garis yang kita cari adalah

Sumber :
http://matematikajitu.wordpress.com/2013/03/17/rumus-praktis-persamaan-garis-lurus/
Jika :
1. Diketahui Gradien, dan titik
Jika diketahui gradien
Persamaan garis lurus yang memiliki gradien
2. Diketahui dua titik
Jika persamaan garis melalui titik
Persamaan garis lurus yang melalui titik (1,4) dan (3,8) adalah …. Jawab:
3. Diketahui Garis dan Titik
Jika persamaan garis
(i)
(ii) Jika sejajar maka
Jika tegak lurus maka
(iii) Melalui titik
Dalam hal ini, ketiga proses tersebut dapat diperingkas dengan rumus berikut:
Garis
|
Garis
|
atau |
atau |
Persamaan garis lurus yang tegak lurus garis
Dari soal kita dapat
Sumber :
http://matematikajitu.wordpress.com/2013/03/17/rumus-praktis-persamaan-garis-lurus/
Langganan:
Postingan (Atom)

